 S
S
"P(E)" is the probability of the event E
P(E) =
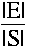
so note that an impossible event is the empty set, and P(
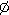 ) = 0
) = 0
furthermore P(S) = 1
Sally invites a distinct set of three of her n bridge-playing friends over for bridge every Wednesday evening for two years (104 Wednesdays). How large must n be (at least)?
#include <stdio.h>
int main()
{
int i, j, k;
for (i = 0; i < n; i++)
for (j = i+1; j < n; j++)
for (k = j+1; k < n; k++)
printf("%d,%d,%d\n", i, j, k);
return 0;
}
(compile with, for example, "cc -Dn=5 whatever.c";
"-Dn=5" on the command line is like
"#define n 5" in the code)
This doesn't answer the question, but it explores it. We can make it count the triples instead of outputting them by changing the code to:
int numtriples(int n)
{
int i, j, k, count = 0;
for (i = 0; i < n; i++)
for (j = i + 1; j < n; j++)
for (k = j + 1; k < n; k++)
count++;
return count;
}
Then:
int main()
{
int n;
extern int numtriples(int n);
for (n = 0; numtriples(n) < 104; n++)
;
printf("Sally needs at least %d bridge-playing friends.\n", n);
return 0;
}
You could call this experimental programming.
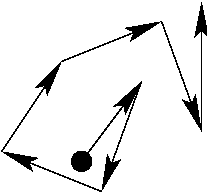
Suppose we start from a given point, then take "steps" in a random direction, repeatedly. Each step is the same size -- call it one metre.
What will be the distance between the starting point and the point we reach after 'n' steps?
Obviously, on average we're back where we started...
But looking only at the absolute distance, since the distance is never negative, and rarely exactly zero, the average will be positive.
As 'n' grows, so does the average distance.
This is an old problem called the "drunkard's walk".
How can we find some average distances for 'n' steps?
A program which makes a step in a random direction, repeatedly, and calculates where we are, is called a simulation of the drunkard's walk. No walking actually takes place! But we find out what would happen if we did walk.
But just doing it one time will be no good. You get a number. Suppose it's 3.108734586123. What does that mean? Another time it's 4.087634586, then 1.2345876... So?
The point is, if you really make random choices, you'll get a different answer every time.
We're interested in the average expected distance. We can do a large number of runs and average them, and as the number of runs goes to infinity, the limit of the average is the actual theoretical expected average. If we do a large enough number of runs, we can probably get pretty close to the actual theoretical average. Although if our random number generator is any good, there's always a chance that we're far off. But the larger the number of runs, the more likely we are to be close, for any definition of close (that is, a tighter definition of close requires a larger number of runs to be as probable, but it's always achievable).
It turns out that the answer to the drunkard's walk problem is a little less than the square root of the number of steps. After 900 steps of one metre, on average we'll be a bit less than 30 metres away from the starting point.
There is an analytic solution, but it's very complex. If this problem were to arise today, with computers we could very quickly get an empirical solution, long before someone had the necessary flash of insight to be able to come up with an analytic solution.
This kind of analysis of a problem like this is called a "monte carlo" method, because that's a famous gambling establishment and this is rather like spinning a large number of roulette wheels, or something like that. Really, "monte carlo method" just refers to the fact that it involves randomization and the behaviour you get when you average a large number of random trials.
Here is a
short program to compute a table of values.
Also discussed in the ninth problem session.
What should be the effect of a pedestrian pushing a button for the crosswalk? Should it make the opposing cars get a yellow light (and then a red light) starting immediately?
What happens when we consider several intersections in a row along the main street of a small town? Often the lights are "timed" between intersections, so that cars have to wait for a green light at the first intersection they hit while going through the town, but after that, as it turns green, the next intersection's light will turn green the right number of seconds later such that as you drive through the town, all the lights turn green for you as you go along.
How does the pedestrian crosswalk button interact with this? How harmful is it to the progress of cars through the town if the light reacts immediately like this to the pedestrian crosswalk button, as opposed to just waiting until it's time for the next change in sync with the rest of the lights?
Perhaps we shouldn't even have a pedestrian crossing button, if it's not going to do anything at all.
Or perhaps it should only work late at night, when the light only turns red upon demand. During the daytime, the button won't do anything because the traffic light will turn red, and the pedestrian crossing light turn to 'walk', only on schedule.
--
All of these decisions have consequences for the efficiency of the system. Small changes can create big traffic jams.
How do we investigate before building the system? Or how do we try out many possibilities, without having to build them all?
We write a simulation.
All the pedestrians, cars, and so on are "objects" in an object-oriented programming language. Not to say you can't write simulations in non-object-oriented programming languages, and people have done so for decades, but we decided that this was a good point to switch to C++ in this course because the simulation can work out quite nicely in an object-oriented programming language.
Then we need some sort of event-processing loop which sees which event happens next (a car arrival, a pedestrian arrival, a car departure, etc), and processes it somehow.
The main purpose is to keep statistics: the number of cars and pedestrians, how long they waited, that sort of thing.
At the end of the program we print a statistical report. It's probably pretty short.
We run it for a long time so that the random fluctuations average out.
We also run it a bunch of times and use our human judgement as to whether we're really observing something other than randomness.
We run it for the various different configurations and get an idea of which are better. There could be conflicting criteria here! One person on the committee might think it's more important to get the cars through, one person might think it's more important that the pedestrians don't have an unreasonably-long wait. But you may find a configuration which fares pretty well on both counts.
--
We distinguish time-driven simulations and event-driven simulations. This traffic light simulation we would write as an "event-driven" simulation, same as assignment three.
That is, we keep looking for the next event. The loop is about events. If no pedestrians arrive for two hours, according to our random selection, and there are no cars during that interval either, then we can just jump ahead to two hours later. We don't have a loop which counts off the seconds. That wastes a lot of time, and also results in a loss of precision.
Here's a time-driven simulation example.
Suppose we're demolishing a building and we need to know for how far around we need to clear traffic, pedestrians, etc. That is, as the building collapses, how far will the stuff "throw"?
There are some random factors involved here in terms of which bits of concrete hit other bits of concrete as they tumble down. A simulation could give us an idea of what is the likely maximum throw distance, which is harder to estimate analytically than the average throw distance.
But what are the events in such a simulation? We don't have any events; there are continuous movements.
So we divide time into tiny steps, and make some simplifying assumption about how things will travel during those tiny steps. Perhaps we assume straight lines. At a given time, we can calculate all the forces: the initial force, gravity (assumed constant), friction in both dimensions, collisions which are occurring with other bits of concrete. Then we can calculate the total force vector and thus where it will be, and with what velocity, in the next time increment.
The calculation is known to be inaccurate because we are projecting it in straight lines, thus implicitly assuming that the forces do not change during that quantum. But the limit as the quantum size goes to zero is the formulas we believe to be correct, so we may be able to get a usable answer if the tiny time steps are small enough.
I wrote a whimsical example illustrating the difference between time-driven and event-driven simulations at http://www.dgp.toronto.edu/~ajr/270/eve/example/simtype/. (But it requires some of the randomization notes below before it makes sense.)
There are good pseudo-random number generators (PRNGs) and bad PRNGs.
PRNGs are algorithmic, hence not truly "random"; but they can be made random-seeming enough for some purposes, such as simulations.
We want to select an event with a particular probability. We want to say, for example, that something has a chance of .3 of happening. We also want to select things with certain distributions, for example a pedestrian will arrive some time in the next ten minutes, with a certain probability distribution.
Laplace in the late 1700s defined the probability of an event as the number of matching outcomes divided by the number of possible outcomes. E.g. throwing a die -- 6 possibilities. If we want to know the probability of getting a 1 or a 2, this is two possibilities out of 6, or 1/3.
We call this a "uniform random selection": a selection from a set of possible outcomes such that each has equal probability of occurring.
We list probabilities on a scale from zero to one;
We have a sample space: the set of all possible outcomes. For example, for throwing a die it's {1,2,3,4,5,6}. We also have a particular event we're interested in, which in Laplace's definitions is a subset of the sample space.
E  S
S
"P(E)" is the probability of the event E
P(E) = 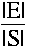
so note that an impossible event is the empty set,
and P(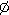 ) = 0
) = 0
furthermore P(S) = 1
This is only valid for uniform selections.
In C:
rand() returns a random non-negative integer.
#include <stdlib.h>
...
int dieroll()
{
return rand() % 6;
}
This only works for a very good PRNG.
For example, suppose that rand() usually returns even numbers.
Then our dieroll() will also usually return even numbers.
There's another way to do this which works for a PRNG which is merely "good" (as opposed to "very good"), to be discussed below.
The Laplacian approach to this is to consider the pairs.
In other words,
Let D = {1,2,3,4,5,6}
S = { (x,y) such that x,y 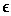 D }
D }
E = { (x,y) such that x,y 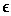 D and x+y==6 }
D and x+y==6 }
= { (1,5), (2,4), (3,3), (4,2), (5,1) }
so P(E) = 5/36
int roll_two_dice()
{
return rand() % 6 + rand() % 6;
}
(There's a strange C thing going on here which bears explanation.
The evaluation order of those two calls to rand() is undefined; the leftmost
rand() invocation may be substituted with either the first or second call to
rand(). But since we're adding together the two results,
it doesn't matter. This code would be non-standard-conformant if it did
matter.)
A "random variable" is a function which maps the outcome of an experiment (event) to a real number. That is, we associate each roll of the pair of dice with a number from 2 to 12 which is the total of the number of spots showing on the top.
A "probability distribution function" is a function which gives the probability p(xi) that the random variable equals xi, for all xi.
p(xi) = P(X = xi)
For all i, 0 <= p(xi) <= 1
The sum over i of p(xi) = 1
Continuous uniform selection: want a random real value in [0,1)
Different versions of rand() return numbers in a different range. They all start at 0; goes up to 215-1 originally, some people have switched to 231-1,....
The ANSI C committee didn't think they could clean this up but they mandated a constant RAND_MAX in stdlib.h. This "max" value is inclusive, so add one.
double uniformrand()
{
return rand() / (RAND_MAX + 1.0);
}
Note that it's crucial that the division be performed in floating-point arithmetic. But it is indeed performed in floating-point arithmetic, because the denominator is floating-point, because we've written the "1" literal as a floating-point literal.
Also note that it's crucial that the addition RAND_MAX + 1 is performed in double-precision floating-point. First of all, it had better not be performed with integer addition, because RAND_MAX may well be the maximum possible integer, and often is. Secondly, converting it to single-precision floating-point may lose accuracy because an integer can often represent more significant digits than can "float". But again, since 1.0 is a literal of type double in C, we indeed have double-precision addition.
Now, what would be a good model for traffic arrival in that small town?
We don't want to say it's uniform amongst, say, 0 to 5 minutes. Maybe we want the possibility of having no cars for a while sometimes. Actually, it seems that there should be no upper limit to the inter-car interval, but it just gets less and less likely.
For continuous random variables, we have a "probability density function". We need this because P(X=x0) = 0 for most of them! e.g. for a uniform random selection in [0,1), p(.3) = 0.
The probability density function is the function f(x) such that
P(a <= X < b) = the integral from a to b of f(x) dx.
The function values themselves are
like a local probability... proportional to
the width of the rectangle you're looking at... specifically, it is the
probability density.
Must have:
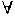 i
i
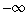 to
to 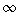 of f(x) dx = 1
of f(x) dx = 1
Examples: uniform [0,2] (constant y=0.5 from 0 to 2, 0 elsewhere]
wackier function describable this way. [draw slightly wacky curve]
Cumulative probability distribution function: FX(i) is the probability that X<=i
The cumulative probability distribution function is the integral of the probability density function. for continuous random variables. For discrete random variables, we don't have a probability density function; a probability density function gives us a probability of zero, or one over infinity if you prefer, for each actual point so it is intrinsically continuous.
Use of cumulative pdf?
Want to map uniform [0,1) to selection along prob density function.
e.g. we pick 0.3.
show on flat & on wacky prob density fn how the integral is 0.3 at a certain
point, 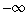 to here.
So when uniform r.v. says 0.3, we can pick here.
to here.
So when uniform r.v. says 0.3, we can pick here.
Now, draw cumulative probability distribution function.
Two examples:
- for the uniform on [0,2), line from (0,0) to (2,1)
- for the wacky, approximate it, ends up at 1.
If we have our uniform selection [0,1), what we want is simply the inverse of this function!
show by choosing 0.3 on the y axis, how this relates to the previous selection of the 0.3 integral spot (since this function is the integral of the previous), and then find the x.
So we've found the inverse, by going from y to x instead of x to y.
Now, back to that small town traffic light example for the last time: If a car arrives on AVERAGE every five minutes, this is the exponential distribution.
Exponential distribution: fX(t) =
e-t, if t >= 0
0, if t < 0
fX(t) is the probability density function for the time between consecutive events if they occur at a particular average rate. What rate? Well, we usually throw some 'r's in there, for rate. We'll fix up the average rate later because it's way easier this way, and its only disadvantage is some substantial lack of formality and actual mathematical proof, but if you want to trust me on this, let's do it the easy way. Then, read the notes about it in the readings, or any other reference, which does it the more sound way. In the exponential distribution, probabilities decay asymptotically towards zero. No positive value is impossible, but huge ones are extremely unlikely. Low values are more likely.
If f(t) is e-t, then
FX(x) (the cumulative probability distribution function for this probability
density function)
= integral 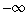 to x of f(z) dz
to x of f(z) dz
= integral 0 to x of e-z dz
(since the integral from
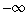 to 0 is zero;
i.e. evaluate the 'if')
to 0 is zero;
i.e. evaluate the 'if')
The indefinite integral of e-z is just -e-z (plus a
constant), so substitute x and
0 for the definite integral:
= -e-x - (-e-0)
e0 is 1, so we have -ex minus minus one, or plus one
= 1 - e-x
Now, as we observed before, we want to go backwards; this is a formula for 'y' in terms of 'x', and we actually HAVE y, y is the cumulative probability, [0,1), and what we WANT is 'x', the time interval until the next car arrives.
If g(x) = y = 1 - e-x,
e-x = 1 - y
take the natural log of both sides, "ln"
-x = ln(1-y)
x = -ln(1-y)
If we take the log of this random variable in [0,1), it's going to look kinda
like this...
log(1) = 0 [explain],
log(0)=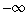 (explain)...
(explain)...
What we want looks more like this: [draw]
If we have a uniformly-distributed random variable in the range[0,1), then 1-x
is a uniformly-distributed random variable in the range (0,1], and ln(1-x) is
in the range (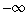 ,0], so
-ln(1-x) is in the range
[0,
,0], so
-ln(1-x) is in the range
[0,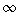 ).
And it has the
right distribution.
).
And it has the
right distribution.
More or less. We can't talk about the maximum value or the range now, but still, if we multiply this by different numbers, we'll get different distributions.
We talk about the MEAN of the random variable. The reason for sticking with base 'e' is that the mean turns out to be 1.
So if we want, just to take a completely arbitrary example, a waiting time with exponential distribution and a mean of two million microseconds, we can multiply by 2000000.
Waiting time with exponential distribution and a mean of 2000000:
double exp2Mrand()
{
return -log(1 - rand() / (RAND_MAX + 1.0)) * 2000000.0;
}
Also have to include math.h for this. log() is in the math library. It is the natural log, i.e. log base e.
The "rate" you'll see in the usual presentation of this is the reciprocal of the mean. The "rate" is higher for more arrivals and that "*2000000" is higher for fewer arrivals, i.e. longer between them.
So you'll usually see "/r" instead of "times something"; the "rate" here would be 0.0000005; it's the same, but the above may be an easier way to think of it.